 emerik
ned 31.5.2009 20:55
emerik
ned 31.5.2009 20:55
Matematika - pomoć
 emerik
ned 31.5.2009 20:55
emerik
ned 31.5.2009 20:55
 lzgr
ned 31.5.2009 21:02
lzgr
ned 31.5.2009 21:02
Na ovoj češ stranici pronaći sve što ti treba.Klikni na 8 razred.
 jurluk
ned 31.5.2009 21:02
jurluk
ned 31.5.2009 21:02

 emerik
ned 31.5.2009 21:04
emerik
ned 31.5.2009 21:04

 jurluk
ned 31.5.2009 21:10
jurluk
ned 31.5.2009 21:10
 emerik
ned 31.5.2009 21:13
emerik
ned 31.5.2009 21:13
O= 3/2·a·(a·√(3)+√(3·a²+4·h²))
to bi trebala biti tocna formula.
da skuzio sam da nisu isti rezultati
ali gle ni udbenik ti nije uvjek tocan
 emerik
ned 31.5.2009 21:26
emerik
ned 31.5.2009 21:26
O= 3/2·a·(a·√(3)+√(3·a²+4·h²))
to bi trebala biti tocna formula.
 jurluk
ned 31.5.2009 21:26
jurluk
ned 31.5.2009 21:26
ne radi se o piramidi, nego o prizmi
ne radi se o piramidi, nego o prizmi
 D_Inuit
ned 31.5.2009 21:35
D_Inuit
ned 31.5.2009 21:35
Ja sam u srednjoj školi, i mogu ti reći sasvim precizno jer sam neki dan pisao ispit.
Znači, oplošje šesterostrane prizme jednako je zbroju baza (2*B) plus pobočju, koje se sastoji od 6 sukladnih pravokutnika (ako me pamćenje ne vara, u osnovnoj se ne uče kose prizme).
Baza je šesterokut, a ako je pravilan, to je onda lik koji se sastoji od 6 jednakostraničnih trokuta, jer je a jednako radijusu opisane kružnice tog šesterokuta.
Zato površina šesterokuta iznosi 6*površini jednakostraničnog trokuta, što je a na kvadrat korijena iz 3, sve kroz 4.
Pobočje ti je 6 puta visina puta a.
sqrt-drugi korijen, ^x je potenciranje
Sve skupa, zbrojeno, jednako je {12 * ([a^2*sqrt(3)]/4) + 6*a*v}
 pajic3
ned 31.5.2009 21:37
pajic3
ned 31.5.2009 21:37
OPLOŠJE PRAVILNE ŠESTEROSTRANE PRIZME GLASI: O=3xa2 x korijen3 +6av
Ovo ti je 1000% točno.
 leo_819
ned 31.5.2009 21:38
leo_819
ned 31.5.2009 21:38
Ja sam u srednjoj školi, i mogu ti reći sasvim precizno jer sam neki dan pisao ispit.
Znači, oplošje šesterostrane prizme jednako je zbroju baza (2*B) plus pobočju, koje se sastoji od 6 sukladnih pravokutnika (ako me pamćenje ne vara, u osnovnoj se ne uče kose prizme).
Baza je šesterokut, a ako je pravilan, to je onda lik koji se sastoji od 6 jednakostraničnih trokuta, jer je a jednako radijusu opisane kružnice tog šesterokuta.
Zato površina šesterokuta iznosi 6*površini jednakostraničnog trokuta, što je a na kvadrat korijena iz 3, sve kroz 4.
Pobočje ti je 6 puta visina puta a.
sqrt-drugi korijen, ^x je potenciranje
Sve skupa, zbrojeno, jednako je {12 * ([a^2*sqrt(3)]/4) + 6*a*v}





 Maxy
ned 31.5.2009 21:39
Maxy
ned 31.5.2009 21:39
Baza ti je kroz 4 a ne kroz 2 ako je pravilan šesterokut tj. B= a2 · √3 / 4
a oplošje je 6 ha
 D_Inuit
ned 31.5.2009 21:41
D_Inuit
ned 31.5.2009 21:41
Eto, hvala vam na potvrdi. Ako se rezultat uvrštenih brojeva ne poklapa s rješenjem danim u zbirci, onda je problem u njoj.
Meni se isto više puta znalo dogoditi da je u zbirci sasvim krivo rješenje, što sam i provjerio s profesorom.
Provjeri gledaš li točan zadatak, nakon određenog broja rješenih zna se dogoditi da rješavaš 47. i provjeravaš s rješenjem iz 48. i sl..
 Maxy
ned 31.5.2009 21:41
Maxy
ned 31.5.2009 21:41

 leo_819
ned 31.5.2009 21:45
leo_819
ned 31.5.2009 21:45
baza je 6 kvadrata a jedan kvadrat je a2sqrt(3) / 4
Alex nije moguće da si opet isto dobio, probaj ponovo
 onaj koji jesam
ned 31.5.2009 21:45
onaj koji jesam
ned 31.5.2009 21:45
samo mo reci kako se pise korjen???
 pajic3
ned 31.5.2009 21:46
pajic3
ned 31.5.2009 21:46
Pogledaj moju formulu koju sam ti napisao.. Kada uvrstiš sve dođe 48korijena3 x 120
Autor je pogriješio!
 Maxy
ned 31.5.2009 21:47
Maxy
ned 31.5.2009 21:47
molim te da mi kazes koji zadatak na kojoj stranici pa cu ti napisati postupak ako mi dobro ispadne
 onaj koji jesam
ned 31.5.2009 21:48
onaj koji jesam
ned 31.5.2009 21:48
za pravilnu sesterostranu ovako je sigurno:
O=3a[a*sqrt(3) + 2h]
/* sqrt je korjen
 pajic3
ned 31.5.2009 21:48
pajic3
ned 31.5.2009 21:48
Ako ti treba riješit još koji zadatak slobodno ga ispiši.. Kolko sam to vježbo mogo sam već i diplomirat 
Pozdrav!
 onaj koji jesam
ned 31.5.2009 21:49
onaj koji jesam
ned 31.5.2009 21:49
Baza ti je kroz 4 a ne kroz 2 ako je pravilan šesterokut tj. B= a2 · √3 / 4
a oplošje je 6 ha
 Maxy
ned 31.5.2009 21:50
Maxy
ned 31.5.2009 21:50
...
 onaj koji jesam
ned 31.5.2009 21:50
onaj koji jesam
ned 31.5.2009 21:50
meni je to pis of kejk ;ja san MIOC
 D_Inuit
ned 31.5.2009 21:51
D_Inuit
ned 31.5.2009 21:51
baza je 6 kvadrata a jedan kvadrat je a2sqrt(3) / 4
Alex nije moguće da si opet isto dobio, probaj ponovo
Ništa od tebe, sine Bille, ili Steve, što te čini sretnijim.
 Bukva
ned 31.5.2009 21:51
Bukva
ned 31.5.2009 21:51
O = 2 · B + P
O = 2 · 3 · (a2 · √3 / 2) + 6 · a · h
(kada stavim kosu crtu to označava razlomak, a u razlomku su samo oni brojevi koje sam stavio u zagradu)
(na kraju smo nešo pokratili i izašla nam je formula za "korištenje"):
O = 3 · a · ( a · √3 + 2 · a · h )
 pajic3
ned 31.5.2009 21:52
pajic3
ned 31.5.2009 21:52
Jao što sam brzoplet, nisam vidio 5 dm
 onaj koji jesam
ned 31.5.2009 21:55
onaj koji jesam
ned 31.5.2009 21:55
MOLIM VAS DA MI POMOGNETE!!!
Idem u 8. razred osnovne škole i imam problem što se tiče matematike!
Imam udžbenik "Matematika 8" u izdanju "PROFIL"-a napisan od strane Tamare Nemeth i Gorana Stajčića, drugo polugodište, prvo izdanje tiskan 2007, ožujak. U utorak pišemo test iz geometrijskih tijela (prizme, piramide, stošci i kugle, te sfere), te sam ja ovaj vikend ponavljao. Zapelo je na šesterostranoj prizmi, točnije na njezinom oplošju.
Na satu, u bilježnicu smo napisali ovu formulu (O = oplošje, P = površina plašta, B = površina baze (pravilni šesterokut), h = visina, a = osnovni brid baze) :
O = 2 · B + P
O = 2 · 3 · (a2 · √3 / 2) + 6 · a · h
(kada stavim kosu crtu to označava razlomak, a u razlomku su samo oni brojevi koje sam stavio u zagradu)
(na kraju smo nešo pokratili i izašla nam je formula za "korištenje"):
O = 3 · a · ( a · √3 + 2 · a · h )
Sada ću napisati formulu za Bazu (B) i za plašt (P) tog istog šesterokuta:
B = 6 · ( a2 · √3 / 4 )
B = 3 · ( a2 · √3 / 2 )
P = 6 · a · h
To su bile formule koje smo zapisali na satu, a ne nalaze se u knjizi. Isto tako imam formule na na papiru od "M.I.M. - SRAGA"-e sa svim formulama koje će mi ikada trebati, a one daju ovakve formule:
B = (3 · a · √3 / 2)
P = 6 · a · h
O = 3 · a2 · √3 + 6 · a · h
Ako pokušavam izračunati zadatak uz pomoć M.I.M.-ovih formula, bez obzira išao samo sa "O" formulom ili kombinirajući 2 · B + P = O, uvijek dobijem isti rezultat, dok kada pokušavam izračunati zadatak uz pomoć formula iz bilježnica, bez obzira išao samo sa "O" formulom ili kombinirajući 2 · B + P = O, uvijek dobim različit rezultat, a jedini rezultat koji je isti sa M.I.M.-ovim rezultatom je ako kombiniram formule iz bilježnice u načinu 2 · B + P = O.
Nadalje... U već prije navedenom udžbeniku na stranici "75" napisane su formule za pravilni šesterokut:
P = 6 · P1
P1 = (3 · a2 · √3 / 2)
Pošto znamo da se površina pravilno šesterokuta izračunava tako da zbrojimo šest površina jednakostraničnih trokuta koji se nalaze u pravilnom šesterokutu ako ga razdijelimo po glavnim dijagonalama dolazimo do zaključka da bi trebali izračunati prvo površinu jednakostraničnih trokuta. Ta formula se u već navedenoj knjizi nalazi na strani "74" i ona glasi:
P = (a2 · √3 / 4)
Ako usporedimo formulu za izračunavanje površine jednakostraničnog trokuta i formulu za izračunavanje površine pravilnog šesterokuta dolazimo do spoznaje da P1, koji u površini pravilnog šesterokuta označava površinu jednakokračnog trokuta nije jednak formuli za izračunavanje površine kod jednakostraničnog trokuta!
Nadalje... Na stranici "94" u već navedenom udžbeniku stoji da za izračunavanje baze kod šesterostrane prizme (izračunava se obujam, ali isto treba prvo izračunati bazu!) piše da je formula za izračunavanje baze ova (Primjer 3., Rješenje:) :
B = 6 · (a2 · √3 / 4)
Kada pogledamo ovu formulu i formulu sa stranice "75" i "74" dolazimo do zaključka da su koristili formulu za izračunavanje pravilnog šesterokuta P = 6 · P1, a P1 zamijenili sa formulom za izračunavanje površine jednakostraničnog trokuta sa stranice "74".
Mene zanima jedna stvar:
KOJA JE TOČNA FORMULA ZA IZRAČUNAVANJE OPLOŠJA PRAVILNE ŠESTEROSTRANE PRIZME???
Molim vas da mi pomognete!!! I tražim pomoć od svih osmaša ili svih ostalih koji se razumiju u to gradivo. Molim bez zloćudnih komentara...
Molim vas pomozite...
Zadatak na kojem sam zapeo "72". h = 5 dm, a = 4 cm, O = ?
RJEŠENJE BI TREBALO BITI: O = ( 24 · √3 + 1200) cm2
MOLIM VAS BRZ ODGOVOR I SLOBODNO PITAJTE AKO NEŠTO NIJE JASNO!!!
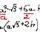
KOJA JE TOČNA FORMULA ZA IZRAČUNAVANJE OPLOŠJA PRAVILNE ŠESTEROSTRANE PRIZME???
Molim vas da mi pomognete!!! I tražim pomoć od svih osmaša ili svih ostalih koji se razumiju u to gradivo. Molim bez zloćudnih komentara...
Molim vas pomozite...
Zadatak na kojem sam zapeo "72". h = 5 dm, a = 4 cm, O = ?
RJEŠENJE BI TREBALO BITI: O = ( 24 · √3 + 1200) cm2
MOLIM VAS BRZ ODGOVOR I SLOBODNO PITAJTE AKO NEŠTO NIJE JASNO!!!